Cours sur les triangles : médiatrices et médianes - 4ème

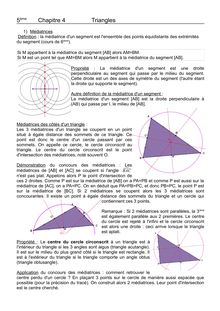
ème5 Chapitre 4 Triangles 1) Médiatrices Définition : la médiatrice d'un segment est l'ensemble des points équidistants des extrémités èmedu segment (cours de 6 ). Si M appartient à la médiatrice du segment [AB] alors AM=BM. Si M est un point tel que AM=BM alors M appartient à la médiatrice du segment [AB]. Propriété : La médiatrice d'un segment est une droite perpendiculaire au segment qui passe par le milieu du segment. Cette droite est un des axes de symétrie du segment (l'autre étant la droite qui supporte le segment). Autre définition de la médiatrice d'un segment : La médiatrice d'un segment [AB] est la droite perpendiculaire à (AB) qui passe par I, le milieu de [AB]. Médiatrices des côtés d'un triangle : Les 3 médiatrices d'un triangle se coupent en un point situé à égale distance des sommets de ce triangle. Ce point est donc le centre d'un cercle passant par ces sommets. On appelle ce cercle, le cercle circonscrit au triangle. Le centre du cercle circonscrit est le point d'intersection des médiatrices, noté souvent O. Démonstration du concours des médiatrices : Les médiatrices de [AB] et [AC] se coupent si l'angle BAC n'est pas plat. Appelons alors P le point d'intersection de ces 2 droites. Comme P est sur la médiatrice de [AB] on a PA=PB et comme P est aussi sur la médiatrice de [AC], on a PA=PC. On en déduit que PA=PB=PC, et donc PB=PC, le point P est sur la médiatrice de [BC].