Exercices sur les nombres premiers
Belgacem
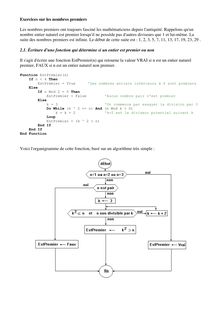
Exercices sur les nombres premiers Les nombres premiers ont toujours fasciné les mathématiciens depuis l'antiquité. Rappelons qu'un nombre entier naturel est premier lorsqu'il ne possède pas d'autres diviseurs que 1 et lui-même. La suite des nombres premiers est infinie. Le début de cette suite est : 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 . 2.1. Écriture d'une fonction qui détermine si un entier est premier ou non Il s'agit d'écrire une fonction EstPremier(n) qui retourne la valeur VRAI si n est un entier naturel premier, FAUX si n est un entier naturel non premier. Function EstPremier(n) If n 0) k = k + 2 'k+2 est le diviseur potentiel suivant k Loop EstPremier = (k ^ 2 > n) End If End If End Function Voici l'organigramme de cette fonction, basé sur un algorithme très simple : Remarque : Si cette fonction est placée dans la feuille de code associée à une feuille de calcul alors elle ne peut être utilisée que par une procédure de cette feuille de calcul. En revanche, si cette fonction est placée dans un module alors elle peut être utilisée depuis n'importe quelle feuille de code et même directement depuis une feuille de calcul comme étant une fonction définie par l'utilisateur ... On peut dans ce cas placer dans la cellule B1 (par exemple) la formule : = EstPremier(A1). 2.2.